Fluid-structure interaction

A wave-energy converter in the ocean

Researchers in the DCML are actively developing new computational methods to treat fluid-structure interaction. This is an important class of problems that has come to the forefront recently with the emphasis on wave energy conversion systems. These systems translate wave motion into structural motion, that is eventually used to generate electricity.

The methodologies that we are currently developing rely on the use of overset grids. The basic approach is to rely on a fixed Lagrangian mesh for the structural domain, superimposed over a background Eulerian grid for the fluid domain. Eulerian elements completely underneath the deformed structural domain do not contribute to the approximation for the fluid velocity and pressure. As the structure deforms, it effectively changes the fluid domain. A simple example of flow over a cantilever is shown in Figure 1. The idea is to avoid remeshing the fluid domain, particularly for problems in which the free surface of the water comes into play, and topology changes are important to capture.

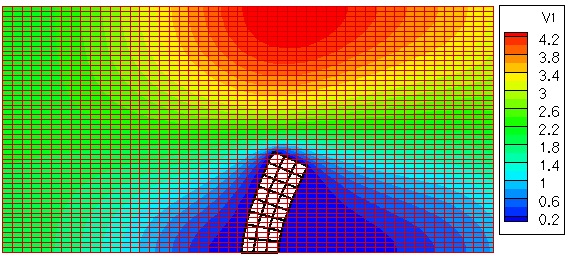
Overset meshes for simulating fluid-structure interaction.

Key questions with this approach include properly enforcing boundary conditions at the solid-fluid interface, and accurately transmitting tractions between the solid and fluid. Over the past few years researchers in the DCML have been developing techniques to do this accurately and robustly. We are currently extending these methods to incompressible fluid flow, transient problems, and free-surface flow. 

 References

  1. Lee C, Dolbow J, Mucha PJ. A narrow-band gradient-augmented level set method for multiphase incompressible flow, Journal of Computational Physics Volume 273, Pages 12-37, 2014
  2. Mourad HM, Dolbow J, and Harari I. A bubble-stabilized finite element method for Dirichlet constraints on embedded interfaces, International Journal for Numerical Methods in Engineering 69 (4): 772-793, 2007
  3. Mourad HA, Dolbow J, Garikipati K. An assumed-gradient finite element method for the level set equation, International Journal for Numerical Methods in Engineering 64 (8): 1009-1032, 2005
  4. Ji H, Dolbow JE. On strategies for enforcing interfacial constraints and evaluating jump conditions with the extended finite element method, International Journal for Numerical Methods in Engineering 61 (14): 2508-2535, 2004